2024. 8. 25. 10:37ㆍ프로그래머스/Kotlin | Level2
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제
문제 설명
콜라츠 추측이란 로타르 콜라츠(Lothar Collatz)가 1937년에 제기한 추측으로 모든 자연수 k에 대해 다음 작업을 반복하면 항상 1로 만들 수 있다는 추측입니다.
| 1-1. 입력된 수가 짝수라면 2로 나눕니다. 1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다. 2.결과로 나온 수가 1보다 크다면 1번 작업을 반복합니다. |
예를 들어 주어진 수가 5 라면 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒2 ⇒ 1 이되어 총 5번만에 1이 됩니다.
수가 커졌다 작아지기를 반복하는 모습이 비구름에서 빗방울이 오르락내리락하며 우박이 되는 모습과 비슷하다고 하여 우박수 또는 우박수열로 불리기도 합니다. 현재 이 추측이 참인지 거짓인지 증명되지 않았지만 약 1해까지의 수에서 반례가 없음이 밝혀져 있습니다.
은지는 우박수열을 좌표 평면 위에 꺾은선 그래프로 나타내보려고 합니다. 초항이 k인 우박수열이 있다면, x = 0일때 y = k이고 다음 우박수는 x = 1에 표시합니다. 이런 식으로 우박수가 1이 될 때까지 점들을 찍고 인접한 점들끼리 직선으로 연결하면 다음과 같이 꺾은선 그래프를 만들 수 있습니다.
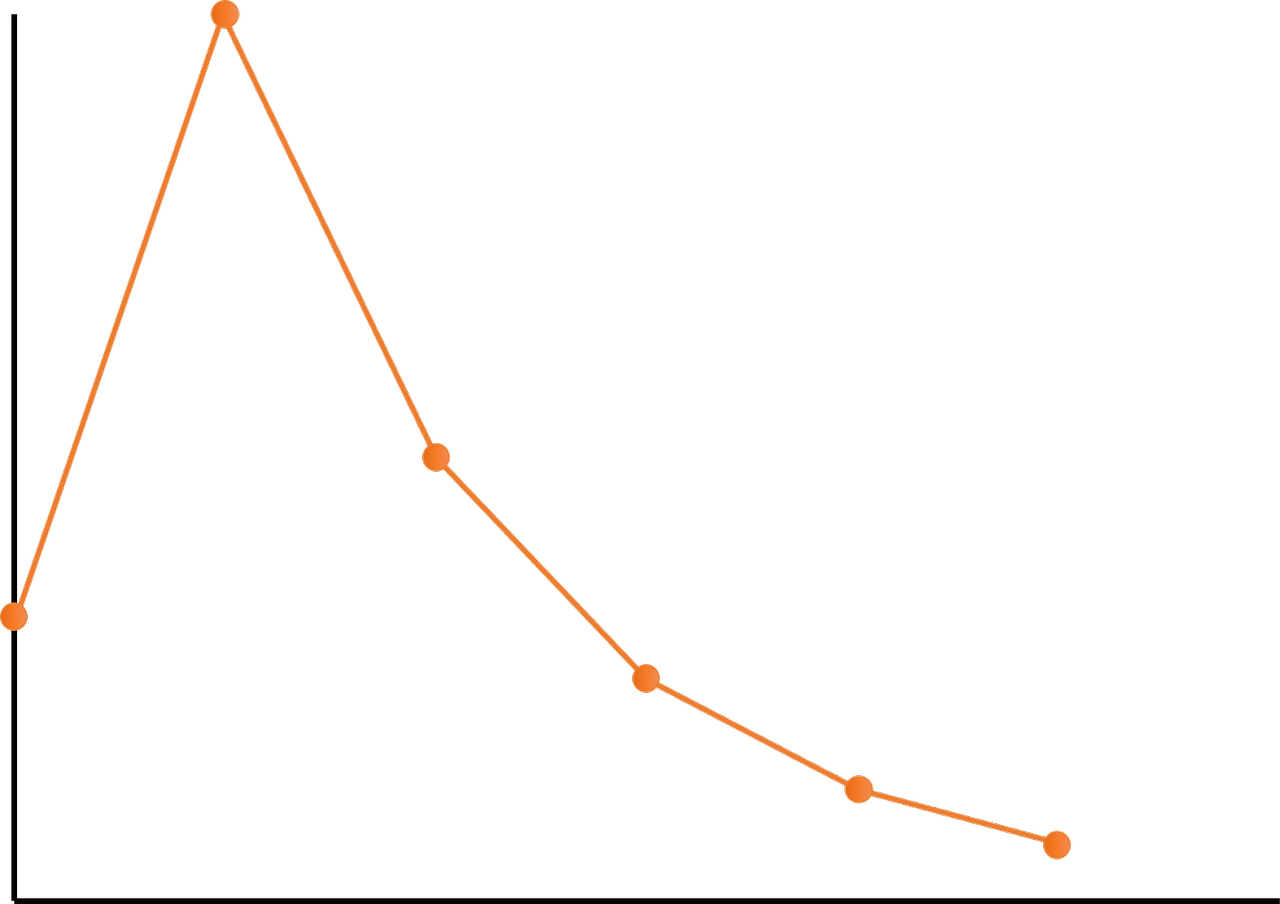
은지는 이렇게 만든 꺾은선 그래프를 정적분 해보고 싶어졌습니다. x에 대한 어떤 범위 [a, b]가 주어진다면 이 범위에 대한 정적분 결과는 꺾은선 그래프와 x = a, x = b, y = 0 으로 둘러 쌓인 공간의 면적과 같습니다. 은지는 이것을 우박수열 정적분이라고 정의하였고 다양한 구간에 대해서 우박수열 정적분을 해보려고 합니다. 0 이상의 수 b에 대해 [a, -b]에 대한 정적분 결과는 x = a, x = n - b, y = 0 으로 둘러 쌓인 공간의 면적으로 정의하며, 이때 n은 k가 초항인 우박수열이 1이 될때 까지의 횟수를 의미합니다.
예를 들어, 5를 초항으로 하는 우박수열은 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 이를 좌표 평면으로 옮기면 (0, 5), (1, 16), (2, 8), (3, 4), (4, 2), (5, 1) 에 점이 찍히고 점들을 연결하면 꺾은선 그래프가 나옵니다. 이를 [0,0] 구간에 대해 정적분 한다면 전체 구간에 대한 정적분이며, [1,-2] 구간에 대해 정적분 한다면 1 ≤ x ≤ 3인 구간에 대한 정적분입니다.
우박수의 초항 k와, 정적분을 구하는 구간들의 목록 ranges가 주어졌을 때 정적분의 결과 목록을 return 하도록 solution을 완성해주세요. 단, 주어진 구간의 시작점이 끝점보다 커서 유효하지 않은 구간이 주어질 수 있으며 이때의 정적분 결과는 -1로 정의합니다.
제한사항
- 2 ≤ k ≤ 10,000
- 1 ≤ ranges의 길이 ≤ 10,000
- ranges의 원소는 [a, b] 형식이며 0 ≤ a < 200, -200 < b ≤ 0 입니다.
- 주어진 모든 입력에 대해 정적분의 결과는 2 을 넘지 않습니다.
- 27
- 본 문제는 정답에 실수형이 포함되는 문제입니다. 입출력 예의 소수 부분 .0이 코드 실행 버튼 클릭 후 나타나는 결괏값, 기댓값 표시와 다를 수 있습니다.
입출력 예
| k | ranges | result |
| 5 | [[0,0],[0,-1],[2,-3],[3,-3]] | [33.0,31.5,0.0,-1.0] |
| 3 | [[0,0], [1,-2], [3,-3]] | [47.0,36.0,12.0] |
입출력 예 설명
입출력 예 #1
- 5로 시작하는 우박수열은 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 그래프에서 꺾이는 지점을 경계로 5개의 구역 넓이를 구하면 각각 10.5, 12, 6, 3, 1.5 입니다.
입출력 예 #2
- 3으로 시작하는 우박수열은 3 ⇒ 10 ⇒ 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 그래프에서 꺾이는 지점을 경계로 3개의 구역 넓이를 구하면 각각 47, 36, 12 입니다.
풀이
나의 풀이
import kotlin.math.abs
import kotlin.math.min
class Solution {
fun solution(k: Int, ranges: Array<IntArray>): DoubleArray {
val answer = DoubleArray(ranges.size)
val collatz = arrayListOf(Pair(0,k))
val area = arrayListOf(0.0)
while (true) {
val index = collatz.last().first
val num = collatz.last().second
if (num == 1) break
val newNum = if (num % 2 == 0) num / 2 else num*3+1
collatz.add(Pair(index+1, newNum))
area.add(abs(num-newNum).toDouble() / 2 + min(num, newNum))
}
val n = area.size - 1
ranges.forEachIndexed { index, ints ->
val a = ints[0]
val b = n + ints[1]
if (a == 0 && ints[1] == 0) answer[index] = area.sum()
else if (b-a < 0) answer[index] = -1.0
else if (b-a == 0) answer[index] = 0.0
else {
var sum = 0.0
for (i in a+1 .. b) {
sum += area[i]
}
answer[index] = sum
}
}
return answer
}
}
- 기초 변수 선언
- 콜라츠 추측을 순서대로 저장할 변수 collatz (index, 숫자 순서로 저장한다.)
- 각 구간 별로 너비를 저장할 area ((0,k)는 0으로 저장)
- 콜라츠 추측
- 반복문을 돌면서 값이 1이 될 때까지 콜라츠 단계를 진행한다.
- 각 구간 별로 면적을 구하는데, 아래 직사각형과 위 삼각형을 각각 따로 구해서 더한다.
- 문제에서 주어진 ranges 별로 면적 구하기
- n은 area 길이 -1 과 같다.
- ranges[0] ≤ x ≤ n+ranges[1]
- 만약 a와 b 둘 다 0인 경우 전체 너비를 리턴한다.
- a와 b의 값이 같으면 0을 리턴한다.
- a의 값이 b보다 크면 -1을 리턴한다.
- 그 외의 경우에는 해당 구간의 면적을 모두 더해서 리턴한다.
Comment
문제를 이해하는 것부터 너무 힘들었… ㅋㅋㅋㅋ
왜 한국어가 더 어려운 것인가…!!
a와 b 범위를 잡는 부분도 헷갈려서 몇 번 틀리고 성공해따… 힣 >//<
'프로그래머스 > Kotlin | Level2' 카테고리의 다른 글
| [프로그래머스/Kotlin]Lv2 - 모음사전 (0) | 2025.01.03 |
|---|---|
| [프로그래머스/Kotlin]Lv2 - 멀쩡한 사각형 (0) | 2024.09.01 |
| [프로그래머스/Kotlin]Lv2 - 리코챗 로봇 (0) | 2024.08.19 |
| [프로그래머스/Kotlin]Lv2 - 당구 연습 (0) | 2024.08.06 |
| [프로그래머스/Kotlin]Lv2 - 점 찍기 (0) | 2024.07.04 |